The main function of NBF is to reduce the third harmonic current in the system. The third harmonic current is the main cause of line energy loss. This part of energy loss is active power. Therefore, as long as this part of the loss is saved, the purpose of saving electricity costs is achieved.
Our idea is to first calculate the active power loss on the line when the system contains the third harmonic current. Then, when there is no third harmonic current in the system, the active power loss on the system line is the difference between the two, which is the loss caused by the third harmonic current. This is also the active power that NBF can save.
1. The loss caused by the third harmonic current in the systemWe use the circuit model shown in Figure 1 for analysis. Make the following assumptions in the analysis:
1 The third harmonic current accounts for 80% of the fundamental current (this is in line with computers, energy-saving lamps, LED screens, etc.)
2 Irrespective of other harmonic currents
3 Irrespective of the effect of skin effect on the wire resistance (frequency of 3rd harmonic is 150Hz, skin effect is not obvious)
4 The cross-sectional area of ​​the zero conductor is equal to that of the phase conductor
5 Single circuit (regardless of the return line) resistance is 5% voltage drop (at rated current), therefore, is: R = 0.05 (U/I), U is the rated voltage (220V), I is the rating of the line Current.
6 The phase shift power factor of the system is 1, that is, active power P=IU.
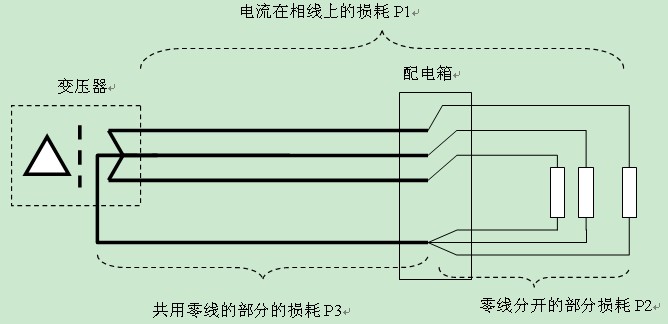
Figure 1 The loss of the third harmonic current in the system
Losses caused by the third harmonic include four parts:
P0: loss of the third harmonic current on the transformer,
P1: Loss of the 3rd harmonic current on the phase line
P2: Loss caused by the 3rd harmonic current on the zero-diving line
P3: Loss of 3rd harmonic current on the common zero line
The total loss P is:
P= P0 + P1 + P2 + P3
Calculation of P0:
Ignore it temporarily.
Calculation of P1:
Including the third harmonic current, the total current effective value is:
I (12+ 0.82)1/2= 1.28I
Its power consumption on the phase line is:
P1 = (1.28I)2X0.05(U/I) = 0.082(IU)
That is, the power consumption per phase line is 8.2% of the single-phase rated power. For a three-phase system, the losses of the three phase lines need to be considered, but this ratio does not change.
Calculation of P2:
If the separated neutral line is short, the resistance is small and can be ignored.
Calculation of P3:
If there is no third harmonic current, the current on the common zero line is 0A. When the third harmonic current is present, the third harmonic current superimposes on the zero line. Because the third harmonic current of each phase is 0.8I, it is 2.4I after being superimposed on the zero line. Therefore, its power consumption on the zero line is:
P3 = (2.4I)2X0.05 (U/I) = 0.288 (IU)
That is, the power consumption on the common zero line is 28.8% of the single-phase rated power. If the three-phase total rated power is considered, the loss on the zero line is 9.6% of the total power.
The total power loss is: P1 + P3, about 17.8% of the total rated power.
2. Saving energy after installing NBFThis section calculates the values ​​of P1 and P3 after installing NBF. The difference between them and NBF is the effect of power saving.
According to the test, after installing NBF, the 3rd harmonic current on the phase and neutral lines can be reduced to about 10%. Therefore, the 3rd harmonic current on the phase line is reduced from 0.8I to 0.08I, and the 3rd harmonic current on the zero line is reduced from 2.4I to 0.24I.
At this time, the loss on the line is calculated as follows.
Calculation of P1:
The total current effective value is:
(12+ 0.082)1/2 ≈ 1
Its power consumption on the phase line is:
P1'=I2×0.05(U/I) = 0.05(IU)
That is, the power consumption on each phase line is 5% of the single-phase rated power, which is mainly caused by currents other than the third harmonic. In three-phase systems, this ratio does not change.
Calculation of P3:
Because the third harmonic current of each phase is 0.08I, it is 0.24I after superimposition on the zero line. Therefore, its power consumption on the zero line is:
P3'= (0.24I)2 x 0.05 (U/I) = 0.00288 (IU)
That is, the power consumption on the common zero line is 0.288% of the single-phase rated power, and if considering the three-phase total rated power, it is 0.096%, which is negligible.
After installing NBF, the total power loss is: P1'+P3', which accounts for approximately 5% of the total rated power.
Therefore, after installing NBF, the power saving effect is:
(P1+P3)- (P1'+P3') = 17.8% - 5% = 12.8%
In the above calculation, the loss P0 of the third harmonic current on the transformer and the loss P2 on the individual zero line are not considered. If these two parts are also included, the potential energy saving is greater. Obviously, it is acceptable to use conservative values ​​as an estimate of energy savings.
3. Supplementary analysisIn accordance with the principle of greater waste, the greater the potential for savings, if the line resistance is smaller, it means less wasted energy, and the effect of power saving is smaller.
Table 1 shows the ratio of power savings when the line voltage drops to different values.
Line voltage drop 2% 3% 4% 5% Saving rate after installation of NBF 2.17% 5.66% 9.23% 12.8%It is also important to point out that the data here ignores the loss of the third harmonic current on the transformer and the individual neutral line. If this part is taken into consideration, the power saving effect can be increased by 1-2%. The specific value is related to the construction of the transformer.
Guangzhou Yunge Tianhong Electronic Technology Co., Ltd , https://www.e-cigarettesfactory.com